穿越时空的涟漪——相对论与引力波
这是我在第98期纽约文化沙龙上的演讲图文稿。引力波的发现再一次引爆了公众对相对论的好奇。如何向外行解释相对论?我不愿用花哨的视效和不知所云的比喻弥补逻辑链的缺失,那些似是而非的字眼只能让大众愈加不明觉厉,对理论物理敬而远之。理解相对论的原理不需要太多物理知识,需要的是对于司空见惯的日常现象的深刻反思。我相信每个人都具备理解相对论的思维能力,他们只需要好的引导。我在这里略去了复杂的数学和物理知识,着重介绍相对论的逻辑 上世纪初,开尔文勋爵在英国皇家研究所向世界宣告,基于牛顿经典力学体系的物理学大厦已经基本完成,唯独被“两片乌云”笼罩着。不到三十年的光景,这两片乌云分别引出量子力学和相对论,将牛顿大厦的基础彻底推翻。
上世纪初,开尔文勋爵在英国皇家研究所向世界宣告,基于牛顿经典力学体系的物理学大厦已经基本完成,唯独被“两片乌云”笼罩着。不到三十年的光景,这两片乌云分别引出量子力学和相对论,将牛顿大厦的基础彻底推翻。
序幕
2016年2月11日,报道最新物理学研究进展的期刊《物理评论快报》(Physical Review Letters)刊登了一篇题为《观测双星黑洞合并产生的引力波》的文章,引起举世震撼。要了解这篇快报说了什么,首先让我们一起回到一百多年前,上世纪初,故事开始的地方。笼罩在牛顿经典物理体系上的两片乌云1900年4月27日,在世纪之交,英国皇家学院的开尔文勋爵说了这样一段话:
“动力学理论认为热和光都是运动的方式,现在这一理论的优美和明晰,正被两朵乌云笼罩着。”
当时是什么情形?基于牛顿经典体系的物理理论已堪称完美,引力、电磁学、光学、热学,都以一种简单、直观的方式描述。物理学的大厦如此坚固,其哲学基础在牛顿的《自然哲学的数学原理》中表述得清晰明了。内部装修是如此的精致,精确解释所有实验观测。它也很优美,许多数学家和物理学家前赴后继地进行数学完善,独辟蹊径地重新表述(例如最小作用量原理),这些视角源源不断地为理论物理学家提供灵感。所以,面对新世纪,物理学家极为乐观——他们认为物理学即将终结,他们的使命已经完成。剩下的工作,无非是通过更精细的实验将物理常数往小数点后多推几位;无非是将理论应用于工程学;无非是拓展化学、生物等 “集邮活动”(卢瑟福语)。然而,正如开尔文勋爵所说,此时物理学大厦还被两朵乌云所笼罩着,意思是当时仍有两个实验无法解释,它们是黑体辐射实验和迈克尔逊-莫雷实验。当然,经典物理并不是第一次面对这样的困难。许多比它们更大的困难都得以顺利解决,让经典力学大厦愈加坚固。然而人们渐渐发现这并不是通常的挫折,这两个实验危机像两个裂口,不但没有弥合,反而被越撕越大,最终彻底替换了物理大厦的理论基础。这两个实验危机引发了风起云涌的物理学革命。大批年轻物理学家在这个舞台上开展了匪夷所思的工作,物理学猝不及防地迎来翻天覆地的变革。黑体辐射实验引出了量子力学。如果没有黑体辐射实验,人们就没有必要去质疑经典力学,没有动机发展一个新的力学。但是,迈克尔逊-莫雷实验是否“引出”了狭义相对论?值得商榷。即使没有迈克尔逊-莫雷实验的诘难,牛顿力学体系仍然存在理论内部的瑕疵,逻辑上是不自洽的。狭义相对论不是被实验所推动的,至少对于爱因斯坦如此。爱氏的相对论和大部分的物理研究不一样,不是建立在实验上,而是建立在逻辑演绎上。后人将他的理论预言和实验观测比较,发现竟然如此一致。
重走爱因斯坦推演相对论之路
“运动的尺会变短”、“运动的钟会变慢”、“时空会被质量弯曲”——你或许在科普书上看到这样的比喻。这些笼统的概念对你理解相对论毫无益处。“时空弯曲”——作为一个有朴素时空经验人,请你告诉我:时空怎么弯曲?时间和空间不是物体,而是一切物体得以存在的容器。所以这个提法是有语病的。但是你反复地看到这句话,便以为自己理解了它。听多了这些比喻,大家会觉得爱因斯坦是个脑洞很大的人。他怎么会想到尺会变短、钟会变慢、时空弯曲?你甚至觉得物理学是天马行空、异想天开的工作。物理学工作确实是富有创造力的,但必须以对世界的直观认识和逻辑演绎为基础。理解相对论的原理不需要太多物理知识,需要的是对于司空见惯的日常现象的深刻反思。我怎么会有时间和空间的观念?怎么会有力的概念?它们来自我的直观感受,还是后天归纳习得的,亦或是教育附加给我的?只有你对一切习以为常的观念进行反思、整理知识的逻辑线,才能真正理解相对论,领会相对论的美,理解爱氏对物理学作出的深刻变革。理解相对论非常、非常困难。首先反思:什么是知识?特别是:什么是物理知识?我们每个人都有一系列的个体经验。这些个体经验以事件序列的形式呈现在我们面前。什么是事件序列呢?比如我是刚出生的小孩,没有任何课本知识。我看到太阳东升西落,即太阳在不同的时间出现在不同的地方——这就是一个事件序列。这只是我个人的经验。借助于语言,不同个体在一定程度上能比较各自的经验,并且发现有些经验是一致的。比如说,一群小孩在一起玩,大家都能做出太阳位置变化的描述,这是一致的经验。再比如,今天你抢我东西吃,我很难受,你很开心,这就不是一致的经验了,所以就不是物理学的讨论对象。所以,物理学就是研究这样一个共同的感觉;物理学客体就是这一类感觉的一种相对恒定的复合。什么是相对恒定?就是某种经验重复地出现:比如太阳每天都在东升西落。古人或许一生只能看到一次流星,在看到第二次之前,他不会把流星当作物理现象来研究,因为它不是一个重复现象。所以,科学是人类心智的产物,因为它是对内心经验的反思和整理。不过,这个观念世界很难完全独立于我们经验的性质之外,正如衣服呈现的形态依赖于人的体形一样。观念世界的形成过程必须依赖于人的经验。这个过程对时间与空间的概念尤为正确。时间与空间是一种恒定的、对所有人一致的观念。这些话不是我说的,是爱因斯坦说的,粗体字摘自《相对论的意义》前言。这本小册子是1922年爱因斯坦在普林斯顿做的四期演讲的整理。现在思考什么是时间,什么是空间。想象一个原始人有一根树枝。他发现这根树枝在什么时候看都是这么长(一种恒定的经验)。于是他截了许多同样长度的树枝,并把它们一段一段连接起来,这样就可以在某个方向上测量任何事件发生的位置,一段树枝就是单位长度的尺,这样能标注事件发生的位置。人们发现只有一个方向的尺子是不够的,至少需要三个方向的尺子,也就是三维。于是,在空间上发生的任何一个事件,可以用这样的方式去描述它:先往X方向走两个单位,往Y方向走三个单位,往Z方向走四个单位,到达某个特定的位置,这个位置被标注为(2,3,4)。这种表述方式必然是唯一的、确定的、没有任何分歧的。这还不够,还需要标注事件发生的时间。人通过太阳的东升西落抽象出一个独立运作的时钟。首先在原点处放这样一个时钟,这还不够,最好在空间的每一个位置都有这样一个时钟。那么当我描述某一个事件发生的时间时,我不用每次都跑回原点看这个钟显示几点,再跑回去。我只要看事件发生地的时钟就行。于是,我们对空间和时间就有了一个完整的概念。你们可以想象这样一个世界,空间上铺满了尺子,每个地方都有完全同步协调的钟。物理学的基本单位是什么?不是电子、质子、质量、能量、力,而是事件(Event),也就是空间和时间的标度:事件 = (空间、时间)。当我们讨论一个物理现象时,必须把它还原到一个事件序列(Event Series)。就是明确地标识,这个物理过程是由哪些事件(Event)组成的,每个事件唯一地在空间、时间中标度出来。参考系,就是可以无歧义地在空间和时间上标度任何一个事件的世界。对于同一个事件,在不同参考系下会出现不同的标度。举个例子,我坐火车从上海出发去北京,途径徐州。这里就出现了两个参考系:一是地面上父母望着我远去的背影,二是在火车上的我。对同样的事件,我和父母的标度方式是不同的。比如,晚上8点,我刚上车就去餐车吃晚饭,在我——车上的参考系看,吃饭事件发生在第二车厢位置(餐车)和8点;在父母看来,因为我从上海出发,这个事件被标度为上海和晚上8点。到晚上11点,车经过徐州,我回5号车厢睡觉了。那么在我看来,睡觉事件发生在第5节车厢的位置和晚上11点;在父母看来,是徐州和晚上11点。所以,同样的事件(吃饭和睡觉)在不同参考系下的标度方式是不一样的。既然参考系是人为规定的系统,具有任意性,那么物理学就不该有优先的参考系。物理理论对所有参考系必须是等价的。思考一个中学物理问题:
一个运动中的物体,如果没有外力施加于它,它将如何运动?A.逐渐变慢最终停止B.保持匀速直线,永远运动下去C.要看其他条件
初中物理告诉我们:选B,即所谓的牛顿第一定律。什么是惯性系?满足牛顿第一定律的参考系叫惯性系。另一方面,牛顿第一定律在惯性系中才满足。这显然是一个循环定义。物理学充满了循环定义,这是逻辑上不可避免的。打个比方,你翻开一本词典,先想一个词,然后去查这个词解释条目中的每一个词,如此进行,最后一定会落回已经查过的词,因为词典的条目是有限的。物理理论也是这样。在这里,我们把它作为基础来接受。也就是说,如果一个物体在没有外力的情况下,它速度大小不变、方向不变、一直运动下去,那么这个参考系是“好的”,特称“惯性系”。 惯性系不是唯一的。如果两个参考系相对作匀速直线运动,例如:在火车上的我(假定火车作匀速直线运动)和地面上的父母。他们观测到的事件序列都满足牛顿第一定律,因此两者都是惯性系。以下是狭义相对论中最重要的、可以说是唯一的基础假设:所有物理定律在所有惯性系里完全相同。也就是说,在火车上的我和在地上的父母不可能通过任何物理实验判断谁在动,谁不在动,谁的速度是多少。注意:上面说物理理论在所有参考系(不仅是惯性系)中都是等价的。“相同”是比“等价”更严格的要求。有人会问:狭义相对论还有一条基础假设:光速是恒定的。这条假设可以还原到第一条假设,因为光是电磁波,而电磁波的传播速度是由物理定律决定的。既然所有物理定律在所有惯性系中完全相同,那么光的传播速度在所有惯性系里一样,是个常数。这有点违反常识。想象我在火车上往前跑,那么在地面看来,我的速度就应该是我实际奔跑速度加上火车的速度——这就是所谓速度叠加原理。但是,如果我是一束光,那么无论从火车上看还是从地上看,我的速度应该是一样的——这当然很反常识。爱因斯坦从十六岁就开始思考这个思想实验:如果我骑在光(电磁波)上,我会看到什么呢?我会看到一个静止的光——既不向前传播,也不向后传播,只是原地振荡。但是,光必须以常数传播。这是理解狭义相对论最困难的地方。我们需要重新思考“时间”和“空间”。首先思考:所谓的“同时”,这种在我们看来是司空见惯的现象,它是绝对的吗?考虑这样一个情况:在一个运动的车上,发生了三个事件。在t=0时,车厢的正中间向车的两边发出两束光, t=1时光走到一半的路程,t=2时光同时达到车厢的两端。但是在地上看来呢?因为车在往前走,车尾是迎着光的,车头是逃离光的。所以在地面的人看来,光先到车尾,后到车头。如果认可光在车上和在地上观测到的速度相同的话,那么在车上“同时”的事件,在地上就不是同时的。
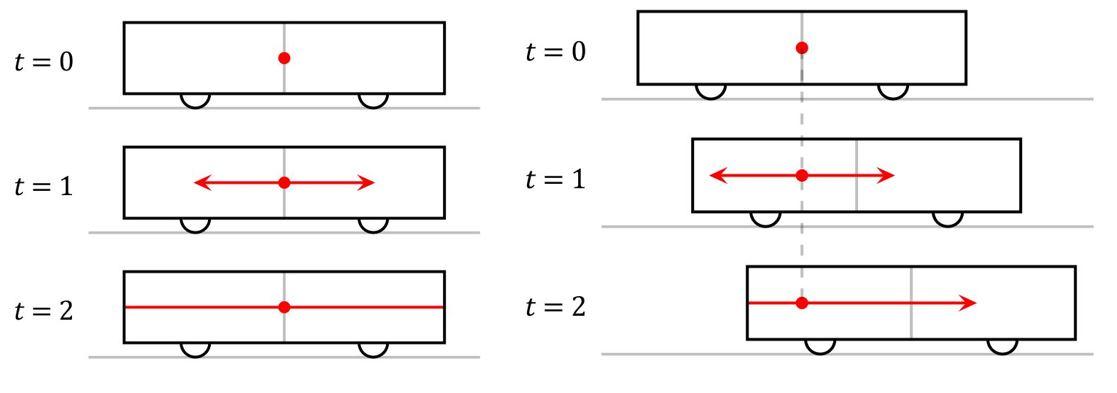
(图片来源:Wikipedia)现在聊聊时间和空间的标度。之前假定存在恒定的尺子,以及在各处协调同步的时钟。在互相运动的参考系之间,这些时钟依然可以完美同步吗?首先考虑如何用一个事件序列表述“测量时间”的概念。既然要保留光速恒定的假设,就用光来校准时钟。考虑一个简单的光子钟模型。地上有一个发出光子的一个仪器,事件1是我在(x,y,z,t)=(0,0,0,0)(即空间在原点,时间为0)发出一束光子。这个光子往上走,遇到一面镜子并返回,对应的事件2是(0,L,0,t),其中L是光子钟的长度(竖直摆放),t是经历的时间。之后光子返回到原点位置,接收器在2t的时候收到一个光子,对应事件3:(0,0,0,2t)。通过三个事件构成的事件序列,我们定义一个“滴答”为事件3和事件1的时间间隔,等于2L/c,c是光速。如果这个钟以速度v向前运动,在地面上的人看来,这个测量行为意味着什么?首先,在地上的人看来,这个光子不是直上直下的,而是经过了一个三角形。由于斜边大于直角边,光在1到2这段时间走过的距离比L长。如果光速不变,我需要更多的时间去完成这样半个滴答t'。直角边长度分别为L和v*t',斜边为c*t',根据勾股定理解得:
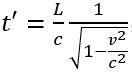
t'比L/c要长。所以,同一个“滴答”事件序列,在车上看和在地上看是不一样的。因此,不存在一个纯粹的,完全一样的时钟。我们必须用某种方式来校准它,而这种校准的方式,在不同参考系将得到不同的结果。不存在一个在全宇宙都同步校准的时钟。所谓的“运动的时钟会变慢”,就是这个道理。
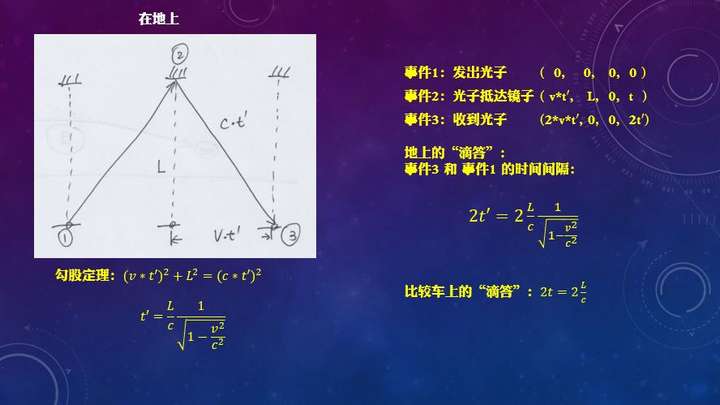
(在上面论证中,不加证明地指出光子钟长度L不会受参考系运动速度v影响,这是因为L所指方向和参考系运动方向垂直。证明可参考《相对论的意义》。)那么长度呢?同样的,使用刚才的光子钟,但这次我把钟横过来放,沿着车行进的方向发射光子,车以速度v往前走,一束光从车厢尾端出发追向前面镜子,抵达镜子并返回车尾。假设我在地上测量到的光子钟长度是L',在地上看来这个过程经历的时间,是光追镜子经历的时间,以及从镜子返回车尾经历的时间。这两个时间加起来,等于地上测量到的“滴答”(2t')。如此计算,我们得到:
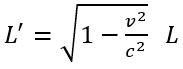
L是在车上看到的尺的长度。因此,在地上的人看来,(运动方向上的)长度被压缩了,这就是所谓的“运动的尺会变短”。 因此,“长度”的概念也必须基于事件序列,而不是理所当然地假定为常数。
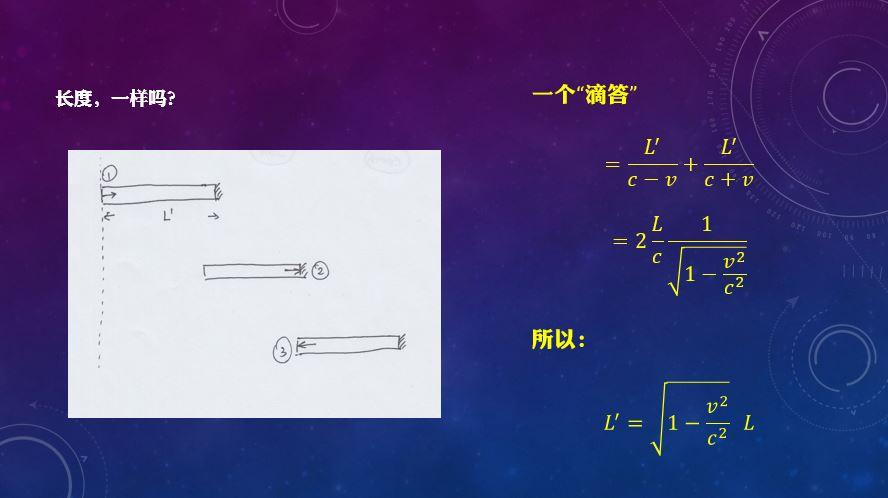
究竟如何在不同参考系中标度同一个事件?牛顿认为存在一个绝对的、真实的、自身永恒流淌的时间,你不管在哪儿测量都一样。比如说,你八点吃饭,那就是八点,你在地上的人和在车上的人看来都是八点。但是爱因斯坦说,这个假设必将和光速恒定相矛盾。所以必须放弃绝对时间,而是通过一种操作定义来校准时间。操作定义是物理学的核心思想,也是物理学区别于科学哲学的重要特征。操作定义是指,对一切物理学概念(时间、长度),必须还原成事件序列,再作讨论。不定义事件序列,就不要空谈是否存在绝对时空。同一个事件在不同参考系里,时间和空间的标度是不一样的,具体的变换过程要用到洛伦兹变换,数学好的同学可以自己去查甚至推导一下。注意:我们在这里谈的是对时空的一个新的定义,基于光速不变的校准方式。只有在这样一个新的定义下,“光速不变”,也就是所谓的“惯性系等效原理”才能得到保留。狭义相对论先聊到这里。你或许会问:怎么没讲那个著名的质能公式E=mc^2?通过刚才的逻辑演绎,你可以理解,爱因斯坦对质量、能量、动量做了重新定义(就像对时间和空间一样)。因此,质能公式里的“质量”、“能量”和牛顿体系中的“质量”、“能量”的定义是不同的。爱氏并不是发现了质量和能量的新的关系,而是重新定义了质量和能量,两者在新的定义下满足质能公式。感兴趣的朋友可以去看推导过程,其逻辑和我们讨论时间空间的逻辑是一样的。
广义相对论
时间不同于空间,它永恒流淌。你可以轻而易举地判断两把尺子是不是等长:把它们的一端重叠在一起,看另一端的位置是否相同。但你如何判断两次相继的心跳经历的时间是否一样?不可能把第二次心跳的开始移回到第一次心跳的开始,然后一起等待下一个心跳。你可以用钟啊!问题是,你如何证明钟走过的“每一秒”是等长的呢?我们可以通过约定一把特定的标准尺来定义“一米”;但是,我们怎么可能约定一个特定的“标准秒”来定义“一秒”?如果有的话,那么这一秒已经发生了,还是即将到来,还是恰好发生在你读这句话的一刻?没有一种时间的定义方式优于另一种,它们在逻辑上是等价的。老赵信奉太阳,他把太阳的东升西落定义为一天。爽姐只信自己,她把每一次心跳定义为一秒。老赵的世界里存在这样一条规律:
“在运动时人的心跳变快”。
爽姐的世界里存在这样一条规律:
“运动中的一天经历的时间(心跳次数)更长”。
彭加勒(法国数学家)指出,这两个规律是等价的,没有哪一个比另一个更正确。时间的测量是一种约定。人们之所以选择一种时间测量而不是另一种,仅仅因为在这个约定下,世界的秩序更简洁,甚至更美。于是爱因斯坦的约定取代了牛顿的约定,因为它保留了惯性原理,也就是:所有物理定律在所有惯性系里完全相同。这么看来,惯性系似乎优于其他参考系。那么非惯性系中的世界满足什么物理规律呢?既然参考系是一种人为规定的系统,那么是否存在一个物理理论,它不依赖于任何参考系呢?这个问题触及到了万有引力的本质。堪称天启的广义相对论如果你还记得牛顿第二定律:F = m × a力 = 惯性 × 加速度物体质量越大,越难推动它。有趣的是,牛顿的万有引力也是和质量成正比的,其中M和m是互相吸引的物体质量,r是距离,G是万有引力常数:
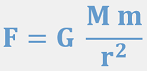
这两个公式告诉我们,地球上的物体无论轻重,自由下落的加速度是一样的,都等于9.8(米每秒平方)。于是,爱因斯坦设想了“封闭电梯”思想实验。请感受一下:
- 地面上的静止的电梯 v.s. 太空中加速上升的电梯
假设我被关在一个封闭的电梯里。第一种情况:我在地球上静止,我能感觉到重力。另一种情况:这个电梯在太空中(所谓太空中是指没有任何星体的引力)作向上的加速运动。作为电梯中的人来说,他都感觉到一种力量在往下拉。他无法区分这两种情形。
- 地面上失重下落的电梯 v.s. 太空中静止的电梯
第一种情况:电梯在地面上失重下落,此时电梯里的人失重,感受不到重力。第二种情况:电梯静止在太空中,没有引力。由于电梯是封闭的,电梯里的人无法区分这两种情形。于是,爱因斯坦提出等效原理:引力和加速运动参考系(非惯性系)的效果是一样的。惯性系和非惯性系有本质区别吗?在地面上,失重加速下落的电梯显然是非惯性系;在太空中静止不动的电梯当然是惯性系,但他们是等效的。等效原理指出,我们无法通过物理实验区分引力和非惯性系。我可以把引力场看成一个非惯性系带来的运动学效果,也可以反过来。爱因斯坦继续思考,究竟什么是惯性系?最方便的假设,就是在自然状态下,做自由落体(Free Fall)的参考系(比如地面上自由下落的电梯)。这时,电梯里的人真的感受不到任何引力——因为即使有引力,也被加速度的效果抵消了。也就是说,电梯里不存在引力,满足牛顿第一定律,光的速度也是常数。想象你往空中抛出一块石头,由于引力的效果,在地面上看,它的轨迹是一条抛物线。当我在自由下落的电梯中看这块石头,它没有受到任何力,它的轨迹是直线。于是,同一个运动(事件序列),在两个参考系中获得了不同的时空标度。遵循上一篇(狭义相对论)的逻辑,我需要找出这两个参考系之间的时空变换关系,这个关系决定了两个参考系中的尺和钟如何校准。一旦我找到了这个变换关系,任何引力下的运动轨迹就可以通过将这个变换关系作用于自由落体参考系中的(无引力)运动轨迹来获得。引力的动力学问题成了几何问题。但引力是不均匀的,地球表面不同位置的引力方向是不同的(都指向地心),因此我们不可能构造一个全局的自由落体参考系,不能一劳永逸地通过一个坐标系变换刻画一切受引力影响的运动。因此,在使用等效原理来描述引力下的运动时,我们依然使用自然状态下(有引力)的参考系,称之为“自然参考系”。上述“寻找时空变换关系”的工作,只能在每一个时空邻域里完成,即时间上和空间上都非常微小的区域——这个区域中的引力近似是常数。互相做匀速直线运动的参考系的时空变换关系是洛仑兹变换,那互相之间作加速运动的参考系之间如何校准?这是非常困难的几何问题。我们暂缓这个问题,思考另一个司空见惯的概念:直线。什么是直线?数学上的定义就是空间的x,y,z轴坐标都是时间的线性函数。现在我们从操作定义的角度来重新定义:直线是两点之间距离最短的路径。也就是说,从A到B,我可以走很多路径;对每一条路径,我用尺子一段一段地测量路径片段,加起来得到这条路径的距离。在所有路径中,找到最短那一条,定义为直线。这是一个操作定义,即基于事件序列的定义。路径片段的距离如何定义?在通常的情况下,是由勾股定理定义的。如果我们推广距离的定义方式,使得在新的定义下,距离最短的路径未必是直观上的“直线”,而是,比如说,抛物线。回到刚才的问题。同样的运动,在自由落体参考系中是直线,在自然参考系中是抛物线,它们之间相差一个坐标变换。在自然参考系中,我们可以如此定义距离,使得同一段路径片段在两个参考系中的距离的数值是一样的。那么,在自由落体参考系中距离最短的轨迹(直线),在自然参考系中的距离当然也是最短的。引力的效果是改变了当时当地的距离定义,使得最短路径是抛物线(确切地说,是由引力影响的运动轨迹)。因此,我们完全可以抛弃引力,用每个时空点的距离定义来取代引力的效果。这种定义距离的方式叫做度规(metric)。在狭义相对论中我们得知空间和时间必须融合在一起讨论,所以这里的度规和距离所涉及的都是3+1维。用度规的方式完全替代引力的效果,进而计算物体的运动轨迹,这就是我们通常说的时空告诉物体如何运动。在牛顿引力理论中,引力是由质量产生的;那么在广义相对论中,度规就是由质量产生的。通过万有引力定律,我们可以刻画质量如何决定度规,这是著名的爱因斯坦方程:
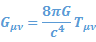
这是一个二阶非线性张量方程。方程的左边是关于度规的一个函数;G是万有引力常数,c是光速,T是能量动量张量——可以理解成物质和能量的密度或强度。在时空的任何一点上,这个方程式都成立。这个方程告诉我们物质如何决定度规,也就是物质告诉时间如何弯曲。你现在可以理解所谓的“时空弯曲”,指的就是在这个定义系里,最短的路径不是直线,而是一条弯曲的线。总结一下牛顿引力和广义相对论的区别:
- 牛顿引力:质量产生引力,引力决定物体运动状态。
- 广义相对论:质量决定时空度规,物体沿最短路径运动。
1919年的日全食实验是最早验证广义相对论的实验之一。(人们对于当时爱丁顿爵士的实验精度是否足以验证广义相对论仍有争议。)大家知道,日全食是指月亮把大部分太阳遮住了,所以在地球上看太阳是环状的。首先根据广义相对论,物体(太阳)改变它周围的度规,使得最短路径不是直线。于是,光的轨迹在太阳附近会发生弯曲。但是大家不要以为牛顿认为光在引力中是不弯曲的。在经典力学中,一切物体都是粒子构成的,一切运动都是粒子的运动,一切作用力都是粒子之间的作用力,所有粒子就有质量,光也不例外,因此光的轨迹也会在引力中弯曲。但是牛顿和爱因斯坦对光弯曲程度的计算结果是不一样的。日全食将告诉我们实际观测更符合哪个理论。通常情况下,遥远星体发出的光经过太阳时发生偏折的效果很难被观测到,因为太阳太亮了,把周围来自遥远星体的光遮盖住了。只有在日全食下,太阳大部分的光被月球遮挡住,我们才能通过照片观测远处星体的位置。这个位置是光偏折后产生的像,由此可推算光的偏折程度。当然,爱因斯坦赢了。今天,人们回顾爱丁顿的实验,质疑仅凭当时的实验精度难以确性地得出这个结论。当然,在之后的许多次日全食观测中,广义相对论的预测得到了精确验证。爱因斯坦发现,还是发明了相对论?不同于大部分物理学家的工作,爱因斯坦完全在理念世界中构建相对论。爱丁顿的日全食观测验证了广义相对论后,有人很兴奋地告诉他:“爱因斯坦博士,您的理论是正确的!”爱因斯坦高冷地回答:“我早知道它是正确的。”对方问:“那如果实验的结果和您提出的理论不一样呢?”爱因斯坦答道:“那非常遗憾,我的理论依然是正确的。”相对论远远超越了它的时代。思考相对论时,我并不感到它试图以科学权威证明它的正确。它只是天启般呈现自己,没有丝毫逻辑上的欠缺或冗余,那种必然和美让人臣服。尽管爱因斯坦最初只是在弱场近似下得到爱因斯坦方程,然而人们发现,这个世界真的是按照他预料的方式运行的,丝毫不差。一百多年来,它经受住了所有实验和天文观测的考验,还发展出黑洞理论、时空奇点、大爆炸理论,可谓历久弥新。请再感受一下这句话:

【本文经纽约文化沙龙 (http://nyshalong.com) 授权转载,首发微信公众号 nyshalong】【转载必须获得主讲人和纽约文化沙龙授权,同时需注明内容来源为:纽约文化沙龙(http://nyshalong.com)】